sönlichen Konsumtionsfonds erweitern. Diese Proportion (Zuwachs II c = Zuwachs I v + Zuwachs I mk) ist die mathematische Grundlage des Akkumulationsschemas von Marx, in welchen Zahlenproportionen wir es auch exemplifizieren mögen.

Wir haben nun nachzuprüfen, ob diese strenge Regel der kapitalistischen Akkumulation den tatsächlichen Verhältnissen entspricht.

Kehren wir zunächst zur einfachen Reproduktion zurück. Das Marxsche Schema lautete, wie erinnerlich:

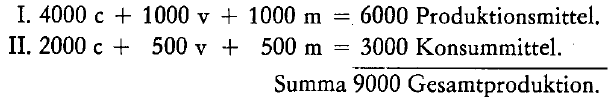
Auch hier haben wir bestimmte Proportionen festgestellt, auf denen die einfache Reproduktion beruht. Diese Proportionen waren:

1. Das Produkt der Abteilung I gleicht (an Wert) der Summe der beiden konstanten Kapitale in I und II.

2. Was sich selbst aus 1 ergibt: Das konstante Kapital der Abteilung II gleicht der Summe des variablen Kapitals und des Mehrwerts in der Abteilung I.

3. Was schon aus 1 und 2 folgt: Das Produkt der Abteilung II gleicht der Summe der variablen Kapitale und der Mehrwerte in beiden Abteilungen.

Diese Verhältnisse des Schemas entsprechen den Bedingungen der kapitalistischen Warenproduktion (reduziert allerdings auf die einfache Reproduktion). So z. B. ist die Proportion 2 bedingt durch die Warenproduktion, d. h. durch den Umstand, daß die Unternehmer jeder Abteilung die Produkte der anderen Abteilung nur im Austausch gegen Äquivalente bekommen können. Das variable Kapital und der Mehrwert der Abteilung I drücken zusammen den Bedarf dieser Abteilung an Lebensmitteln aus. Diese müssen aus dem Produkt der Abteilung II gedeckt werden, doch sind sie nur im Austausch gegen die gleiche Wertmenge des Produkts I, d. h. Produktionsmittel, erhältlich. Da die Abteilung II mit diesem Äquivalent seiner Naturalgestalt wegen nichts anderes anfangen kann, als es im Produktionsprozeß als konstantes Kapital zu verwenden, so ist damit die Größe des konstanten Kapitals der Abteilung II gegeben. Wäre hier eine Disproportion vorhanden, wäre z. B. das konstante Kapital in II (als Wertgröße) größer als (v + m) I, so könnte es nicht ganz in Produktionsmittel verwandelt werden, denn die Abteilung I hätte einen zu geringen Bedarf nach Lebensmitteln. Wäre das konstante Kapital II kleiner